如图,在矩形ABCD中,AB=8,BC=6,对角线AC、BD交于点O,点E在AB延长线上,联结CE,AF⊥CE,AF分别交线段CE、边BC、对角线BD于点F、G、H(点F不与点C、E重合).(1)当点F是线段CE的中点,求GF的长;(2)设BE=x,OH=y,求y关于x的函数解析式,并写出它的定义域;(3)当△BHG是等腰三角形时,求BE的长.https://bgk-photo.cdn.bcebos.com/0b46f21fbe096b6335ab18301c338744ebf8ac24.jpg
如图,在矩形ABCD中,AB=8,BC=6,对角线A
C、BD交于点O,点E在AB延长线上,联结CE,AF⊥CE,AF分别交线段C
E、边B
C、对角线BD于点
F、G、H(点F不与点
C、E重合).(1)当点F是线段CE的中点,求GF的长;(2)设BE=x,OH=y,求y关于x的函数解析式,并写出它的定义域;(3)当△BHG是等腰三角形时,求BE的长.https://bgk-photo.cdn.bcebos.com/0b46f21fbe096b6335ab18301c338744ebf8ac24.jpg
发布时间:2025-07-03 14:58:50
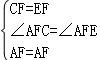 ∴△ACF≌△AEF,∴AE=AC=10,∴BE=2,∵∠CGF=∠AGB,∠GFC=∠ABG,∴∠FCG=∠GAB,∠CBE=∠ABG,∴△CBE∽△ABG,∴
∴△ACF≌△AEF,∴AE=AC=10,∴BE=2,∵∠CGF=∠AGB,∠GFC=∠ABG,∴∠FCG=∠GAB,∠CBE=∠ABG,∴△CBE∽△ABG,∴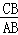 =
=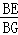 ,即
,即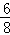 =
=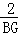 ,BG=
,BG=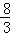 ,∴CG=
,∴CG=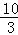 ,∵∠GCF=∠BCE,∠CFG=∠CBE,∴△CGF∽△CBE,∴
,∵∠GCF=∠BCE,∠CFG=∠CBE,∴△CGF∽△CBE,∴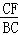 =
=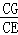 ,又CE=2CF,∴2CF2=BC•CG,∴CF=
,又CE=2CF,∴2CF2=BC•CG,∴CF= ,∴GF=
,∴GF=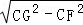 =
=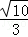 ;(2)如图,
;(2)如图,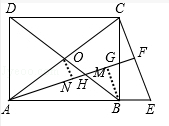 作BM⊥AF,ON⊥AF,垂足分别为M、N,∵AF⊥CE,∴ON∥BM∥CE,∴△ONH∽△BMH,△ANO∽△AFC,△BMG∽△CFG,∴
作BM⊥AF,ON⊥AF,垂足分别为M、N,∵AF⊥CE,∴ON∥BM∥CE,∴△ONH∽△BMH,△ANO∽△AFC,△BMG∽△CFG,∴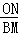 =
=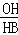 =
= ,
,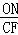 =
= ,
,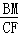 =
=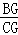 =
=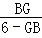 ,∴
,∴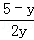 =
=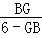 ,又∵△CBE∽△ABG,∴
,又∵△CBE∽△ABG,∴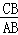 =
=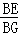 ,BE=x,∴BG=
,BE=x,∴BG=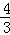 x,∴
x,∴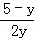 =
= ,则y=
,则y=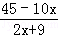 (0<x<
(0<x<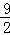 ).(3)当△BHG是等腰三角形,①当BH=BG时,△AHD∽△BHG,
).(3)当△BHG是等腰三角形,①当BH=BG时,△AHD∽△BHG,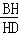 =
=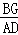 ,则5 y=6,y=1,由y=
,则5 y=6,y=1,由y=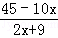 ,解得x=3;②当GH=GB,得出∠AHD=ABH,不存在;③当HG=HB,得出∠HGB=∠HBG=∠OCB不存在.所以BE=3.
,解得x=3;②当GH=GB,得出∠AHD=ABH,不存在;③当HG=HB,得出∠HGB=∠HBG=∠OCB不存在.所以BE=3.