在数列{an}中,a1=8,a4=2且an+2-2an+1 an=0,n∈N*.(1)求数列{an}的通项公式;(2)设Sn=|a1| |a2| … |an|,求Sn.
在数列{an}中,a1=8,a4=2且an+2-2an+1 an=0,n∈N*.(1)求数列{an}的通项公式;(2)设Sn=|a1| |a2| … |an|,求Sn.
发布时间:2025-01-04 11:08:09
在数列{an}中,a1=8,a4=2且an+2-2an+1 an=0,n∈N*.(1)求数列{an}的通项公式;(2)设Sn=|a1| |a2| … |an|,求Sn.
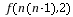 ×(-2)=-n2 9n.当n≥6时,Sn=a1 a2 … a5-a6-a7-…-an=2(a1 a2 … a5)-(a1 a2 … an)=2×(-52 9×5)-[8n ×(-2)]=n2-9n 40.∴Sn=.
×(-2)=-n2 9n.当n≥6时,Sn=a1 a2 … a5-a6-a7-…-an=2(a1 a2 … a5)-(a1 a2 … an)=2×(-52 9×5)-[8n ×(-2)]=n2-9n 40.∴Sn=.