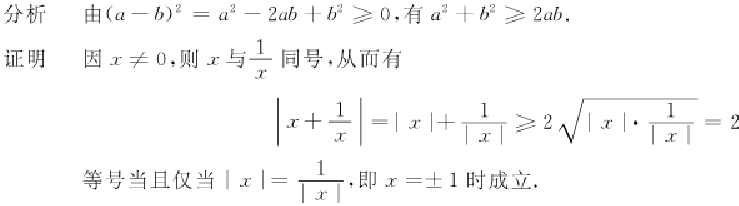4.设x≠0证明x ≥2.并说明其中等号何时成立
4.设x≠0证明x ≥2.并说明其中等号何时成立
发布时间：2025-09-08 06:20:37
请在 下方输入 要搜索的题目：
推荐参考答案 (
由 题搜搜 官方老师解答 )
答案：
相关试题
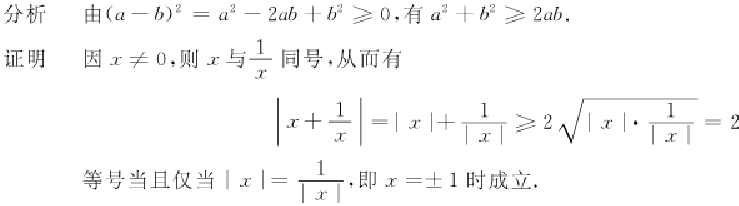
- 1.4.设x≠0证明x ≥2.并说明其中等号何时成立
- 2.4.设x≠0证明x ≥2.并说明其中等号何时成立
- 3.设0＜A、{ x | x ＜ a 或 x ＞ }B、{ x | x ＞ a }C、{ x | x ＞ a 或 x ＜ }D、{ x | x ＜ }
- 4.设f（x）=x（x-1）（x-2），则f‘（0）=______．
- 5.03.设f(x)在[0,π]上连续,且在x=0处可导,证明tim '/(, cos x cos x co nar jdr-(o)
- 6.(集合013)设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a=()
- 7.设集合A={x∈Z|x2﹣4x+3≤0},B={x|log2
- 8.3.设F(X是f(x)的原函数,且F(x)·f(x)=2(1)2.F(0)=1(F(x)>0)求F(x)及fx
- 9.\(设f(x),g(x)是可微函数,且满足u(x,y)=f(2x+5y)+g(2x-5y),\\u(x,0)=\sin {2x},u'_y(x,0)=0,则u(x,y)=(\,)\)
- 10.设f(x)=(x-2π)sinx,x满足大于等于0小于等于π，
