已知函数f(x)=ex ax b.(Ⅰ)若a>0,试判断f(x)在定义域内的单调性;(Ⅱ)当a=-e2时,若f(x)在R上有2个零点,求b的取值范围.
已知函数f(x)=ex ax b.(Ⅰ)若a>0,试判断f(x)在定义域内的单调性;(Ⅱ)当a=-e2时,若f(x)在R上有2个零点,求b的取值范围.
发布时间:2025-01-18 23:51:52
已知函数f(x)=ex ax b.(Ⅰ)若a>0,试判断f(x)在定义域内的单调性;(Ⅱ)当a=-e2时,若f(x)在R上有2个零点,求b的取值范围.
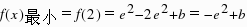 要使函数f(x)在R上有2个零点,则只需
要使函数f(x)在R上有2个零点,则只需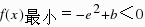 ,即b<e2所以实数b的取值范围为(-∞,e2)
,即b<e2所以实数b的取值范围为(-∞,e2)