P是等边三角形ABC内一点,PC=3, PA=4, PB=5,求△ABC的面积
P是等边三角形ABC内一点,PC=3, PA=4, PB=5,求△ABC的面积
发布时间:2025-05-14 21:32:08
P是等边三角形ABC内一点,PC=3, PA=4, PB=5,求△ABC的面积
 △ABC是等边三角形,
△ABC是等边三角形, AC=AB
AC=AB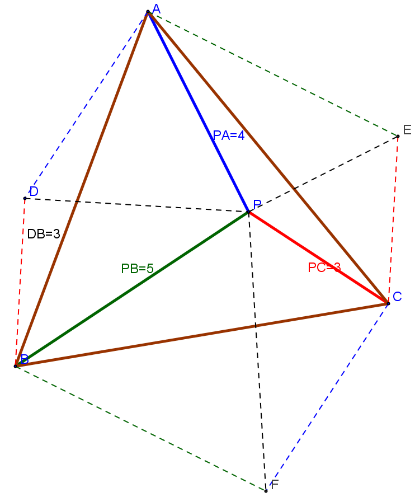
 以A点为中心旋转△ACP至△ABD,即沿AB边做△ABD≌△ACP,连接DP
以A点为中心旋转△ACP至△ABD,即沿AB边做△ABD≌△ACP,连接DP DA=PA=4, DB=PC=3
DA=PA=4, DB=PC=3 ∠DAP=∠DAB 公共角∠BAP=∠PAC 公共角∠BAP=60°
∠DAP=∠DAB 公共角∠BAP=∠PAC 公共角∠BAP=60° 顶角=60°的等腰三角形(DA=PA)是等边三角形,
顶角=60°的等腰三角形(DA=PA)是等边三角形, △DAP是等边三角形
△DAP是等边三角形 DP=DA=PA=4, 又
DP=DA=PA=4, 又 DB=3, PB=5, 据勾股定理逆定理
DB=3, PB=5, 据勾股定理逆定理 △BDP是直角三角形
△BDP是直角三角形 S△ABP S△ACP = S△ADP(等边三角形边长已知) S△BDP(直角三角形三边已知)
S△ABP S△ACP = S△ADP(等边三角形边长已知) S△BDP(直角三角形三边已知) S△ABP S△ACP =3x4÷2
S△ABP S△ACP =3x4÷2 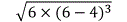 =6 4
=6 4 …………(1);(海伦公式)这样,等边△ABC内被P点分割出的三个计算面积数据不全的三角形中的相邻两个被转换为两个已知三边长的等边三角形和直角三角形求面积。同上,分别以B点为中心,沿BC边做△BCF≌△ABP;以C点为中心,沿CA边做△ACE≌△BCP。连接EP、FP,同理可求得:S S =3x4÷2 =6 …………(2);S△ACP S△BCP =3x4÷2
…………(1);(海伦公式)这样,等边△ABC内被P点分割出的三个计算面积数据不全的三角形中的相邻两个被转换为两个已知三边长的等边三角形和直角三角形求面积。同上,分别以B点为中心,沿BC边做△BCF≌△ABP;以C点为中心,沿CA边做△ACE≌△BCP。连接EP、FP,同理可求得:S S =3x4÷2 =6 …………(2);S△ACP S△BCP =3x4÷2 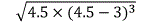 =6
=6 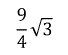 …………(3);S△AB=[(1) (2) (3)]÷2=9
…………(3);S△AB=[(1) (2) (3)]÷2=9 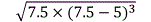
A、ABC
B、abc
C、a_bc
D、ab.c