解:(1)EG=CG且EG⊥CG.
解:(1)EG=CG且EG⊥CG.
发布时间:2025-10-15 21:14:13
解:(1)EG=CG且EG⊥CG.
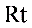 △BEF,∴ ∠EBF=∠DBC=
△BEF,∴ ∠EBF=∠DBC= ∴ B、E、D三点共线,∵ ∠DEF=
∴ B、E、D三点共线,∵ ∠DEF=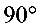 ,G为DF的中点,∠DCB=
,G为DF的中点,∠DCB= ,∴ EG=DG=GF=CG, ∴ EG=CG;∴ ∠EGF=2∠EDG,∠CGF=2∠CDG, (第25题答图1)∴∠EGF ∠CGF=2∠EDC=90°,即:∠EGC=
,∴ EG=DG=GF=CG, ∴ EG=CG;∴ ∠EGF=2∠EDG,∠CGF=2∠CDG, (第25题答图1)∴∠EGF ∠CGF=2∠EDC=90°,即:∠EGC= ,∴ EG⊥CG. ………………………………………………………………………3分
,∴ EG⊥CG. ………………………………………………………………………3分 (2)仍然成立.证明:如图2,延长EG交CD于点H,∵ BE⊥EF, ∴ EF∥CD,
(2)仍然成立.证明:如图2,延长EG交CD于点H,∵ BE⊥EF, ∴ EF∥CD,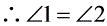
 又FG=DG∴ △FEG≌△DHG,∴ EF=DH,EG=GH∵ △BEF为等腰直角三角形,∴ BE=EF, ∴ BE=DH,∵ CD=BC, ∴ CE=CH,∴ △ECH为等腰直角三角形,又∵ EG=GH,∴ EG=CG且EG⊥CG. ………………………………………………………………6分(3)仍然成立.证明:如图3,延长CG至H,使GH=CG,联结HF交BC于M,联结EH、EC,∵
又FG=DG∴ △FEG≌△DHG,∴ EF=DH,EG=GH∵ △BEF为等腰直角三角形,∴ BE=EF, ∴ BE=DH,∵ CD=BC, ∴ CE=CH,∴ △ECH为等腰直角三角形,又∵ EG=GH,∴ EG=CG且EG⊥CG. ………………………………………………………………6分(3)仍然成立.证明:如图3,延长CG至H,使GH=CG,联结HF交BC于M,联结EH、EC,∵ ∴ △HFG≌△CDG,∴ HF=CD,∠GHF=∠GCD,∴ HF∥CD,∵ 正方形ABCD,∴ HF=BC,HF⊥BC,∵ △BEF是等腰直角三角形,∴BE=EF,∠EBC =∠HFE, (第25题答图3)∴ △BEC≌△FEH,∴ HE=EC,∠BEC=∠FEH,∴ ∠BEF=∠HEC=
∴ △HFG≌△CDG,∴ HF=CD,∠GHF=∠GCD,∴ HF∥CD,∵ 正方形ABCD,∴ HF=BC,HF⊥BC,∵ △BEF是等腰直角三角形,∴BE=EF,∠EBC =∠HFE, (第25题答图3)∴ △BEC≌△FEH,∴ HE=EC,∠BEC=∠FEH,∴ ∠BEF=∠HEC= ,∴ △ECH为等腰直角三角形,又∵ CG=GH,∴ EG=CG且EG⊥CG.……………………………………………………………………8分
,∴ △ECH为等腰直角三角形,又∵ CG=GH,∴ EG=CG且EG⊥CG.……………………………………………………………………8分